O Que É Coeficiente De Correlação?
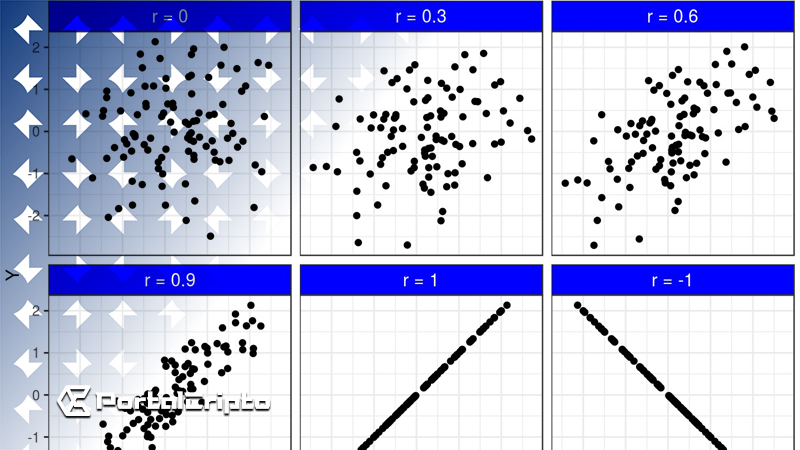
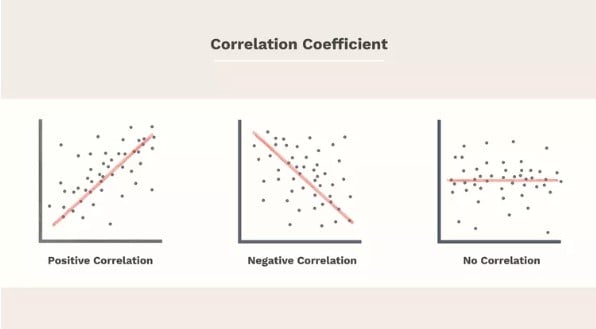
O coeficiente de correlação é uma métrica estatística que quantifica o grau e a direção da relação linear entre duas variáveis quantitativas. Esta métrica pode assumir valores no intervalo de -1 a 1, onde um valor de -1 indica uma correlação negativa perfeita, significando que, à medida que os valores de uma variável aumentam, os valores da outra diminuem, e vice-versa. Um valor de 1 aponta para uma correlação positiva perfeita, refletindo uma relação direta entre as variáveis. Já um valor de 0 denota a ausência de qualquer correlação linear entre as duas variáveis.
Esta ferramenta é amplamente utilizada em diversos campos, como na ciência e no setor financeiro, para medir a intensidade da associação entre dois fatores ou conjuntos de dados. Por exemplo, considerando que preços altos do petróleo beneficiam os produtores, é lógico esperar uma correlação positiva substancial entre os preços do petróleo e os lucros futuros das reservas de petróleo. No entanto, análises históricas revelam que essa correlação pode ser moderada e inconsistente ao longo do tempo.
Como funciona o Coeficiente de Correlação?
Existem diversos métodos para calcular a correlação, sendo o coeficiente de Pearson, ou o “r de Pearson”, um dos mais empregados. Este específico calcula a força e direção da relação linear entre duas variáveis. Contudo, ele não é adequado para capturar relações não lineares ou distinguir entre variáveis dependentes e independentes.
A metodologia do coeficiente de Pearson envolve uma fórmula matemática estatística para avaliar quão próximos os pontos de dados, representando as duas variáveis (com uma plotada no eixo X e a outra no eixo Y), estão de uma linha de regressão ótima. Essa linha é estabelecida por meio de análise de regressão.
Um coeficiente distante de zero, seja positivo ou negativo, indica uma correlação mais forte e um melhor ajuste dos dados à linha de regressão. Valores de -1 ou 1 representam uma correlação perfeita, onde todos os pontos de dados se alinham exatamente na linha, sugerindo uma previsibilidade absoluta entre as variáveis. Quanto mais o valor do coeficiente se aproxima de zero, mais fraca é a correlação, chegando a um ponto em que, a zero, não se observa nenhuma relação linear.
Os critérios para avaliar a força da correlação com base no coeficiente variam conforme o campo de estudo. Em disciplinas como física e química, uma correlação é geralmente considerada significativa se o coeficiente estiver abaixo de -0,9 ou acima de 0,9. Nas ciências sociais, esses limites podem ser mais flexíveis, variando entre -0,5 e 0,5.
Para coeficientes derivados de amostras, a significância estatística é determinada pelo valor p, que leva em conta tanto o tamanho da amostra quanto o valor do coeficiente.
Cálculo do Coeficiente de Correlação
Para determinar a correlação de Pearson, é essencial calcular primeiramente o desvio padrão de cada uma das variáveis e a covariância existente entre elas. O coeficiente de correlação é então obtido pela divisão da covariância pelo produto dos desvios padrão associados a cada variável.
O desvio padrão quantifica a dispersão dos valores de uma variável em torno de sua média, fornecendo uma medida de variação. A covariância, por sua vez, indica se as duas variáveis tendem a variar juntas, ou seja, se movem na mesma direção. O coeficiente de correlação, ajustado em uma escala de -1 a 1, mensura a intensidade dessa tendência conjunta.
Utilização da Estatística de Correlação em Investimentos
O coeficiente de correlação revela-se uma ferramenta valiosa na análise e gestão de riscos associados a investimentos. Conforme os princípios da teoria moderna de portfólio, a diversificação é capaz de atenuar a volatilidade dos retornos de um portfólio, minimizando o risco envolvido. O cálculo da correlação entre os retornos históricos de investimentos pode sinalizar se a inclusão de um novo ativo contribuirá para a diversificação do portfólio.
Além disso, a elaboração de portfólios com base em investimento em fatores, estratégia que visa à montagem de carteiras ancoradas em atributos ligados a retornos acima da média, também se apoia no cálculo de correlações. Traders quantitativos, por sua vez, recorrem a correlações históricas e ao coeficiente de correlação para prever variações nos preços dos ativos no curto prazo.
Limitações do Coeficiente de Correlação de Pearson
É crucial reconhecer que correlação não equivale a causalidade. O coeficiente de Pearson, embora eficaz na identificação de relações lineares entre variáveis, não é capaz de estabelecer a dependência entre elas. Ademais, não especifica que fração da variação em uma variável dependente é explicada por alterações na variável independente, aspecto este mensurado pelo coeficiente de determinação (ou R ao quadrado), que corresponde ao quadrado do coeficiente de correlação.
Este coeficiente tampouco informa sobre a inclinação da linha que melhor se ajusta aos dados, aspecto que pode ser determinado através da técnica de mínimos quadrados na análise de regressão.
Para avaliar relações não lineares ou dados que não seguem uma distribuição normal, o coeficiente de Pearson não é o indicado, sendo suscetível a distorções provocadas por valores discrepantes. Nesses contextos, métodos não paramétricos como o coeficiente de correlação de Spearman, o coeficiente de correlação de classificação de Kendall ou coeficientes de correlação policóricos oferecem alternativas mais adequadas.
Conclusão
O entendimento profundo do coeficiente de correlação e de seu cálculo é fundamental para a análise estatística, oferecendo insights valiosos sobre a relação entre variáveis em diversos contextos, desde a ciência até o setor financeiro. A distinção entre R e R² é crucial, com cada medida desempenhando seu papel específico na interpretação de dados: enquanto R avalia a direção e a força da relação linear entre duas variáveis, R² quantifica o grau em que um modelo explica a variação dos dados observados.
Além disso, o coeficiente de correlação possui uma aplicabilidade prática significativa na gestão de investimentos, auxiliando na mitigação de riscos e na maximização de retornos através da diversificação de portfólio e da adoção de estratégias de negociação baseadas em análises quantitativas. Contudo, é imperativo reconhecer as limitações dessa medida, especialmente sua incapacidade de inferir causalidade e sua sensibilidade a valores discrepantes, o que demanda uma interpretação cuidadosa e o possível complemento com outras técnicas estatísticas para uma análise mais robusta.
Este conhecimento não apenas capacita gestores de carteira e investidores a tomarem decisões mais informadas, mas também enriquece o campo da pesquisa científica, proporcionando uma ferramenta essencial para a exploração de relações entre variáveis. Portanto, o domínio dos conceitos e das técnicas de cálculo do coeficiente de correlação é um ativo valioso em diversas áreas, contribuindo para o avanço do conhecimento e para a eficácia na gestão de recursos e investimentos.
Perguntas Frequentes
R e R² são equivalentes?
Não, R e R² diferem significativamente em suas aplicações dentro da análise estatística. R é o coeficiente de correlação de Pearson, utilizado para avaliar tanto a intensidade quanto a direção da relação linear entre duas variáveis. Por outro lado, R², conhecido como coeficiente de determinação, serve para medir a capacidade de um modelo em explicar a variabilidade dos dados, indicando o quão bem os valores ajustam-se ao modelo proposto.
Qual é o procedimento para calcular o coeficiente de correlação?
O cálculo do coeficiente de correlação é efetuado através da identificação da covariância entre as variáveis em análise, seguido pela divisão desse valor pelo produto dos desvios padrão das respectivas variáveis. Esse processo resulta na quantificação da correlação linear, expressa em uma escala de -1 a 1, entre os elementos analisados.
Qual é a função do coeficiente de correlação no âmbito dos investimentos?
No setor de investimentos, o coeficiente de correlação é instrumental para o manejo eficaz dos riscos associados a um portfólio de ativos. Gestores de fundos de investimento, por exemplo, analisam os coeficientes de correlação entre diferentes ativos para mitigar riscos e controlar a volatilidade do portfólio. Esta prática permite uma gestão mais informada e estratégica das alocações de ativos, visando otimizar os retornos ajustados ao risco.